I had originally published this post on my earlier website and am republishing it here with slight variations.
Epicycloids and hypocycloids offer unlimited artistic possibilities while requiring only a rudimentary knowledge of trigonometry and coordinate geometry. Because of this reason they seemed to be the perfect place to get started I first started exploring Python’s matplotlib package for its animation possibilities. I found Jake VanderPlas excellent series of articles on this topic extremely useful in the initial stages.
In the near future I shall upload my python codes as a github repo. As of now I want to in this post present certain animations I obtained relating to these curves. In the first part I shall discuss hypocycloids, their equations and some animations, in the second part I shall discuss the same for epicycloids, and in the third will show some further animations with both hypocycloids and epicycloids.
The hypocycloid and its equation¶
A hypocycloid is the path traced by a point on the rim of a circle that is rolling without slipping on the interior of another, fixed circle. The figure below illustrates this.
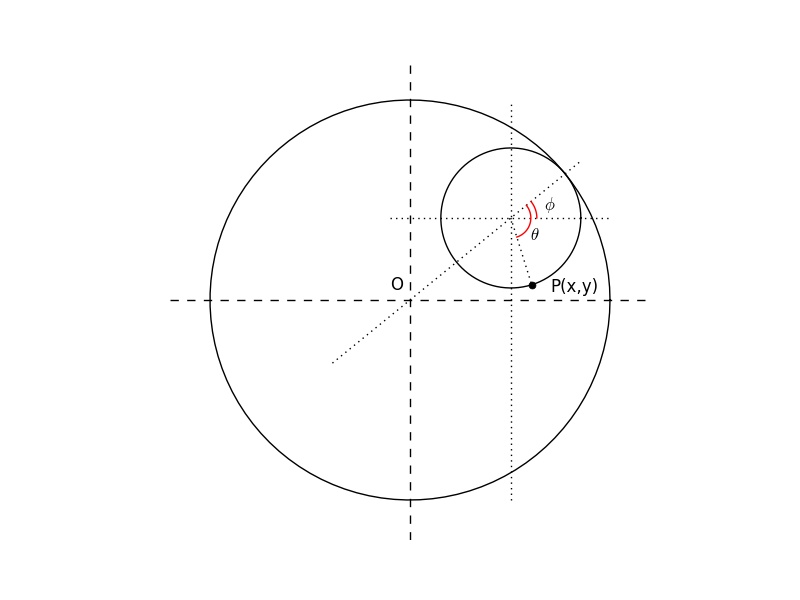
Fig. 1
The fixed circle has radius R and the moving circle has radius r. P is point fixed to the rim of the moving circle. If initially P lay on the intersection of the fixed circle and the x-axis, the condition of no slipping gives
\begin{equation} r\theta = R\phi \label{noslipping} \end{equation}
It then follows from the figure that the equation for the point P is
\begin{eqnarray} x &=& (R-r)\cos\phi + r\cos\left[ \left( \frac{R}{r} - 1\right)\phi\right] \nonumber \\ y &=& (R-r)\sin\phi - r\sin\left[ \left( \frac{R}{r} - 1\right)\phi\right] \end{eqnarray}
Animations¶
Let us have a look at some animations now. Suppose that $\theta = 2n\pi$ and $\phi = 2m\pi$, where $n$ and $m$ are integers. This means that the center of the moving circle completes $m$ revolutions in the same time that it takes the point P to touch the fixed circle $n$ times (not counting the initial position) till it is back to the original position. From the no-slipping condition (Eq. (1)), it follows that
\begin{equation} nr = mR \end{equation}
To be concrete, let us consider the case $r=2R/5$, i.e. $n=5$ and $m=2$. In this case the rolling wheel generates the following hypocycloid (hypocycloid_spokes_v2.py):
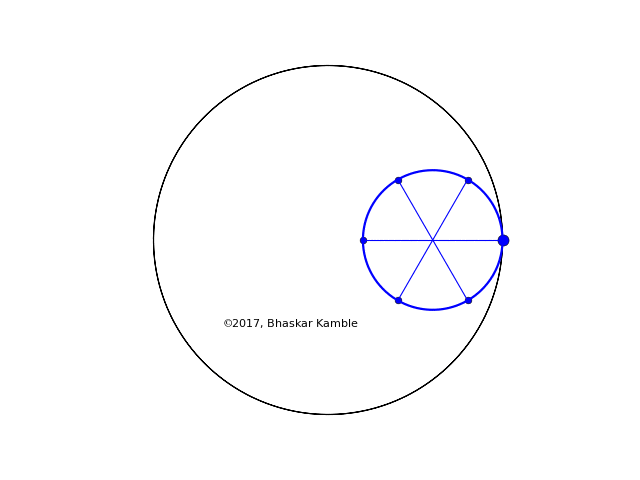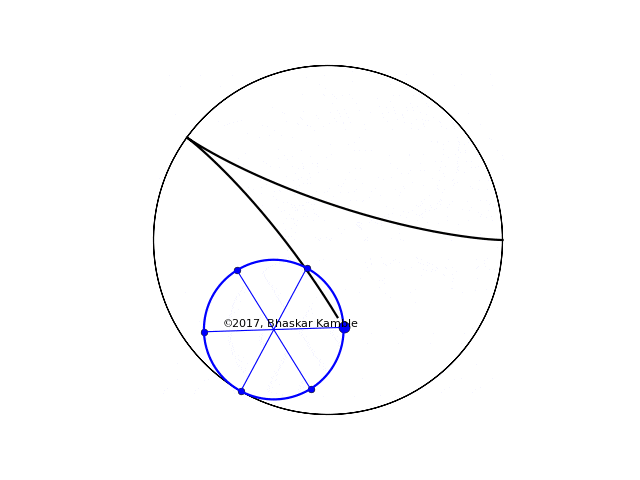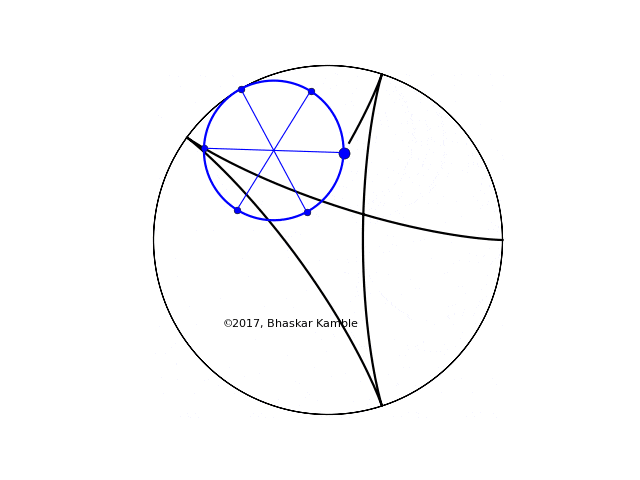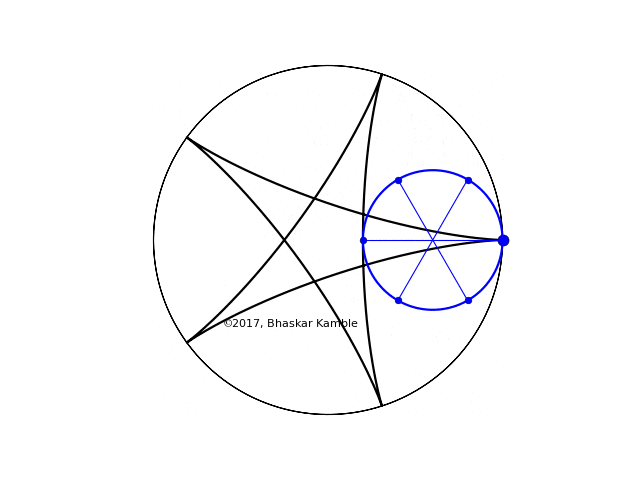
Fig. 2 with $r=2R/5$
Now suppose that $r = 3R/5$, i.e. $n = 5$ and $m = 3$. Funnily enough the curve generated is the same!
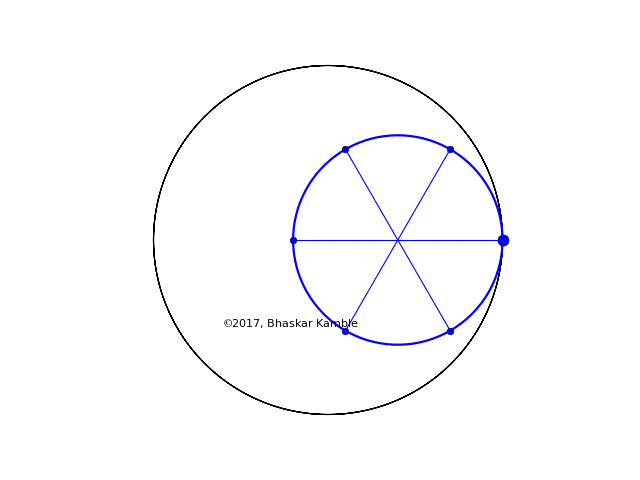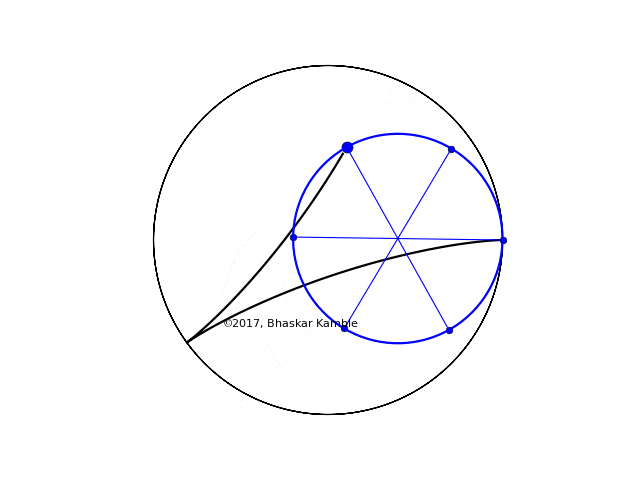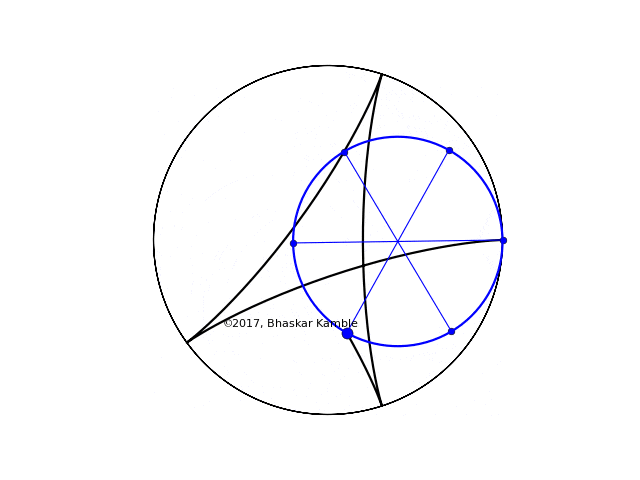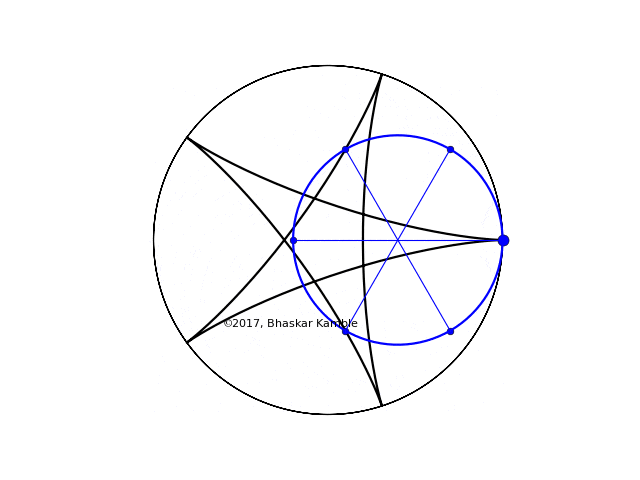
Fig. 3 with $r=3R/5$
I show the above two cases once again, but this time simultaneously (hypocycloid_simultaneous_4_new.py). In the first of the following two animations (Fig. 4), the sense of rotation of the two circles is the same while in the second (Fig. 5) they are opposite. Notice how in Fig. 4 the respective points on the circles tracing out the curve are symmetric with respect to reflections about the x-axis whereas in Fig. 5 they always coincide:
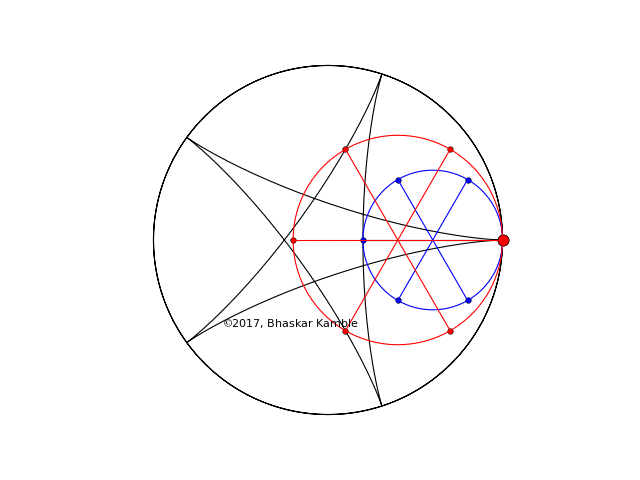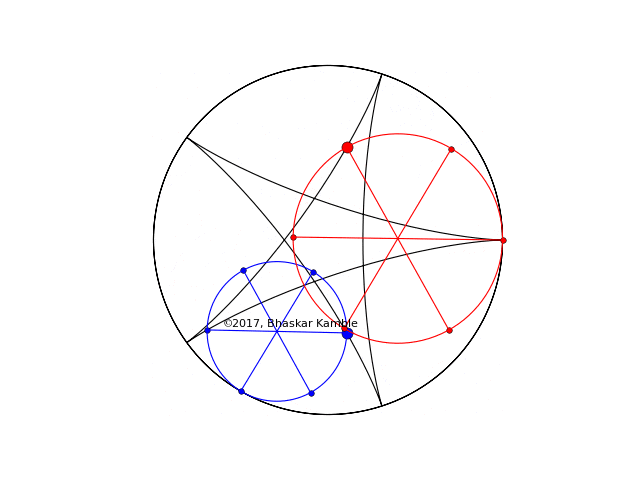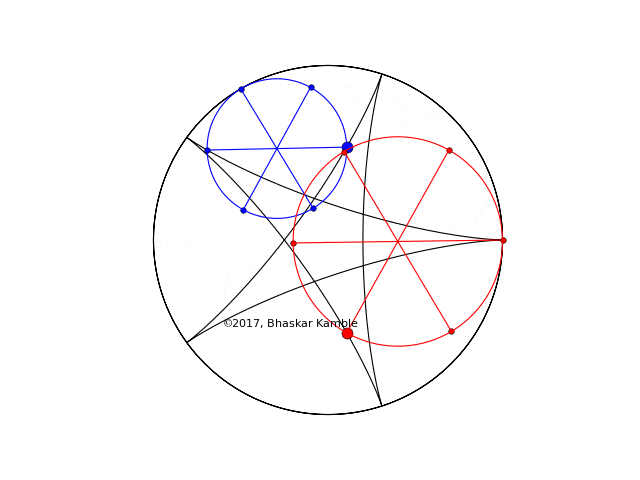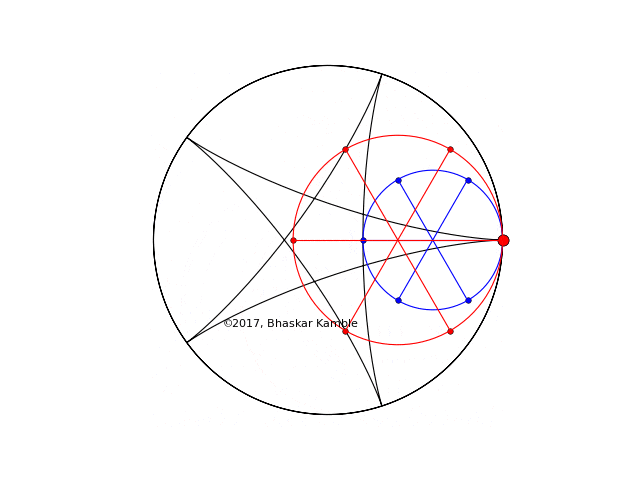
Fig. 4 with $r_1=2R/5$ and $r_2=3R/5$
and (hypocycloid_simultaneous_opp_4_new.py):
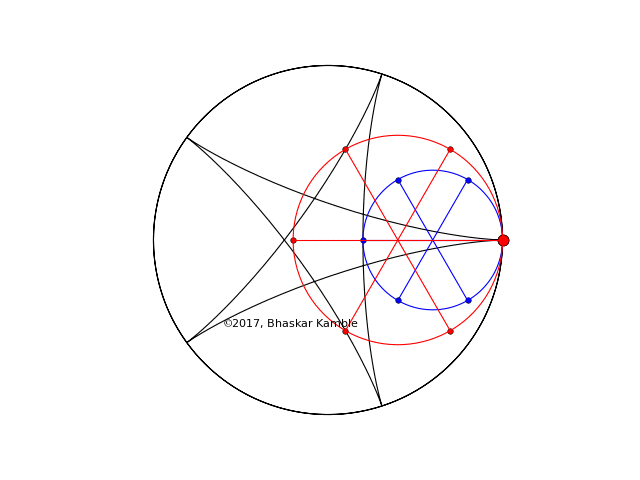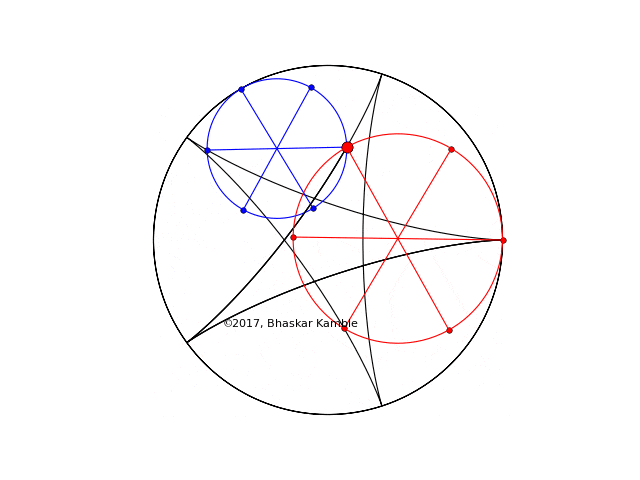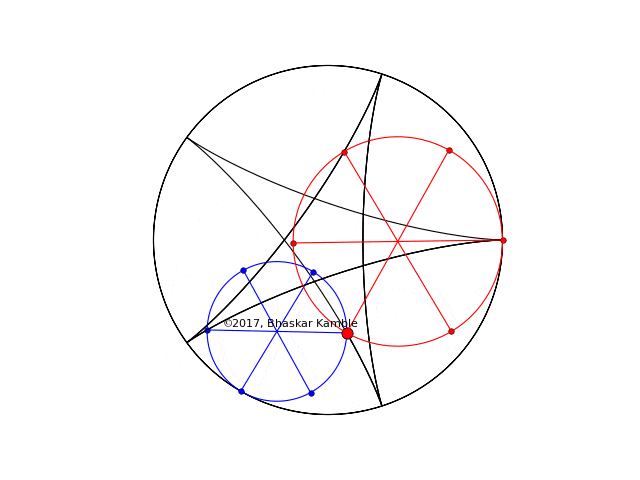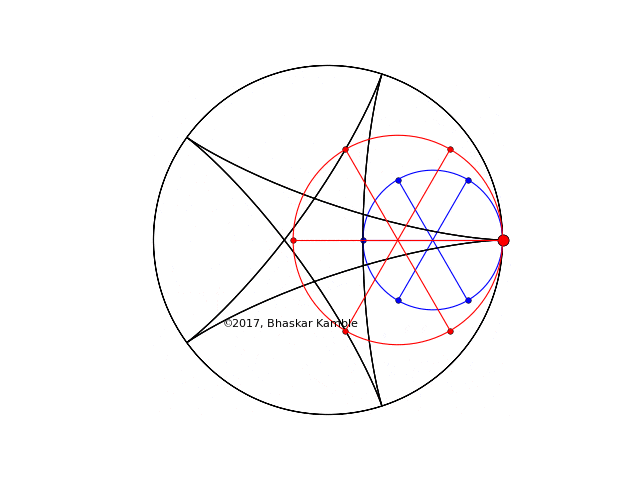
Fig. 5 with $r_1=2R/5$ and $r_2=3R/5$ and the circles rotating in the opposite sense
In the same way the cases $r = R/5$ and $4R/5$ also generate the same hypocycloid, as the following animation shows. (produced by hypocycloid_simultaneous_2_new.py):
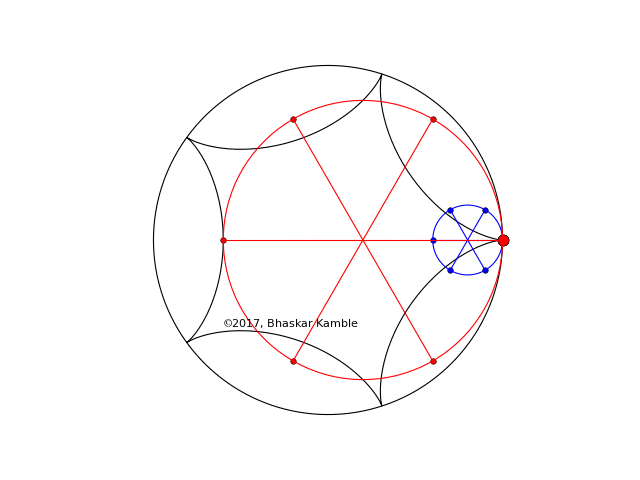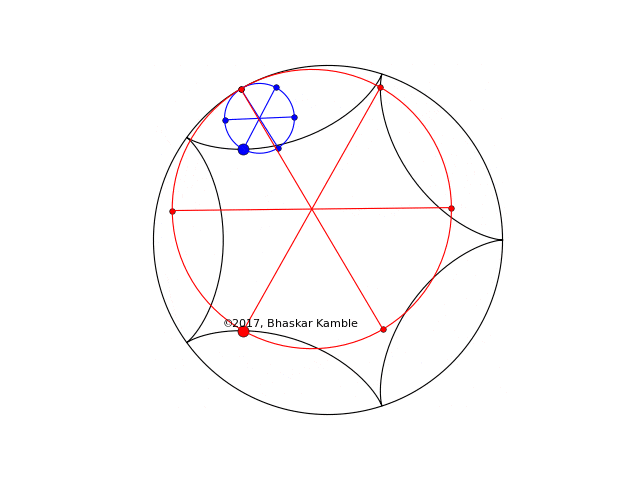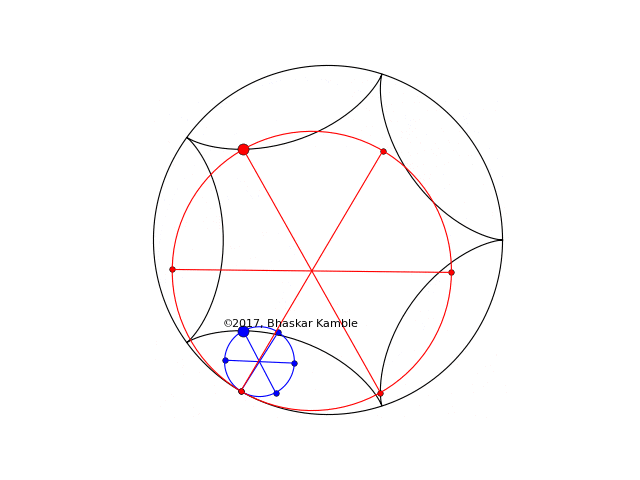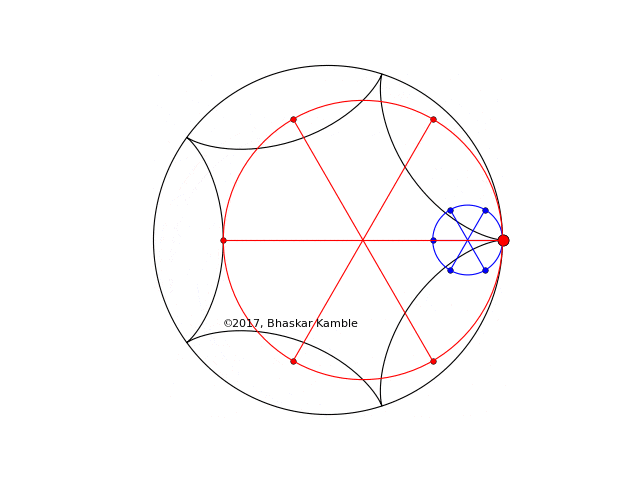
Fig. 6 with $r_1=R/5$ and $r_2=4R/5$
As in Fig. 4 and 5 if the sense of rotation is opposite, the figures coincide, as shown in the following figure (produced by hypocycloid_simultaneous_opp_4_new.py)
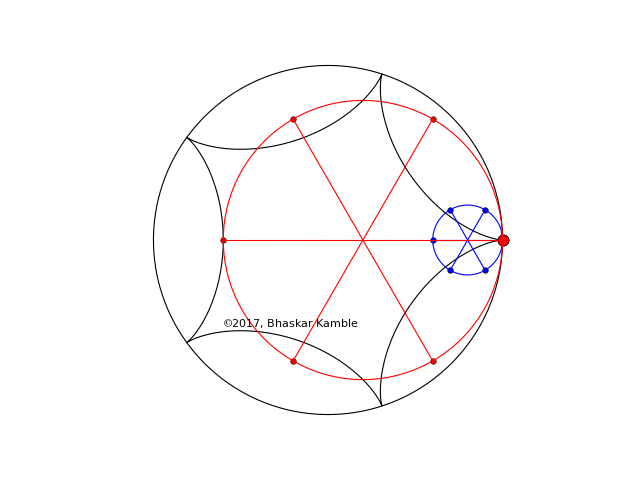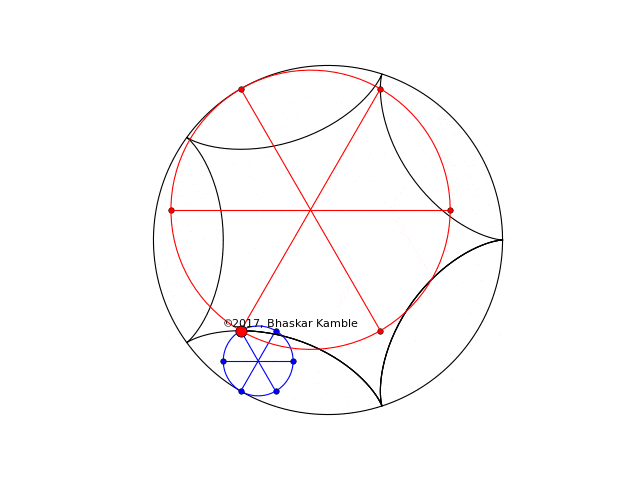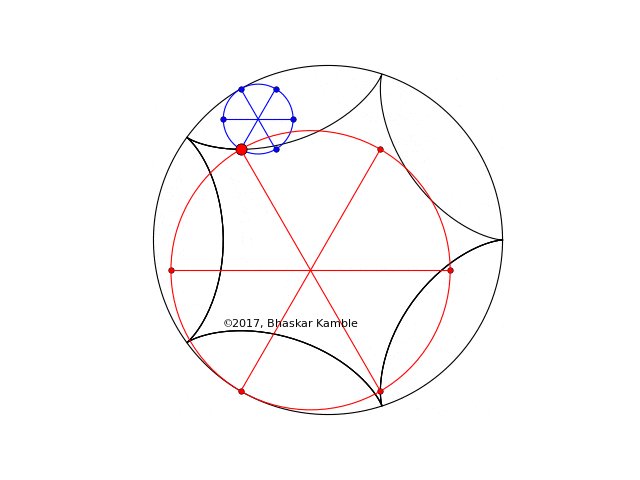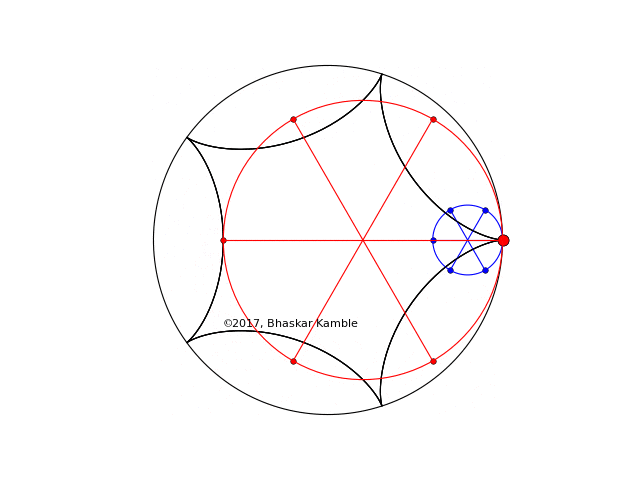
Fig. 7 with $r_1=R/5$ and $r_2=4R/5$ with the circles rotating in the opposite sense
We can summarize a few salient features of the above case of $n = 5$. If we require the moving circle to be smaller than the fixed circle, and allow $m$ to take only integral values, then the possible values of $n$ are 0, 1, 2, 3, and 4. Of these 0 is the trivial case, and of the remaining four non-trivial cases, only two give unique curves. This is reminiscent of traveling waves on a system of infinite identical masses connected with springs and following periodic boundary conditions. In this case it will be remembered that if the masses repeat their motion every $N$ number of masses, where $N$ is odd, then there are $N$ normal modes. Of these, one is the trivial mode and the remaining $N – 1$ non-trivial normal modes are traveling waves with exactly $(N – 1)/2$ unique frequencies with two normal modes (one a wave in the positive direction and the other a wave in the negative direction) for each frequency. This is also reminiscent of the combinatorics formula $^nC_r=^nC_{n-r}$.
In general, when the sum of the radii of the moving circles equals the radius of the fixed circle, then the hypocycloids generated by a point fixed on the rim of the circles will be the same.
Here are a few further cases (produced by hypocycloid_simultaneous_opp_4_new.py). Fig. 8 shows the case $r_1=4R/11$ and $r_2=7R/11$ while Fig. 9 shows $r_1=R/7$ and $r_2=6R/7$
Fig. 8 with $r_1=4R/11$ and $r_2=7R/11$
Another example:
Fig. 9 with $r_1=R/7$ and $r_2=6R/7$
The case of $r = R/2$ is also interesting, in that the resulting curve is simply a straight line:
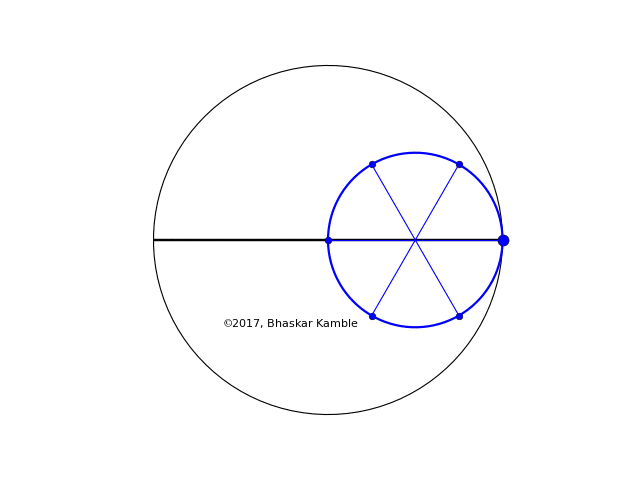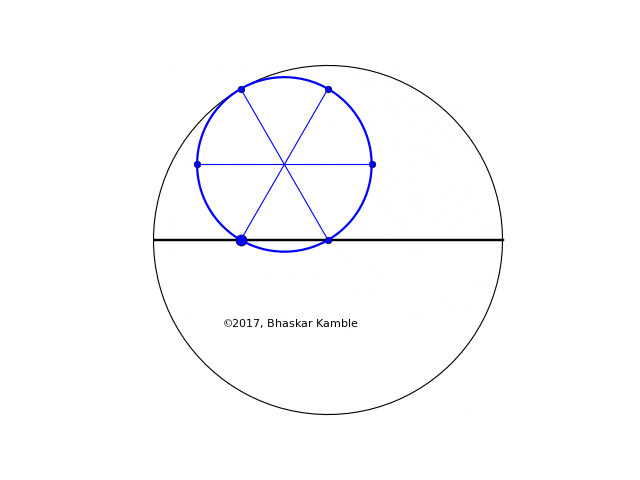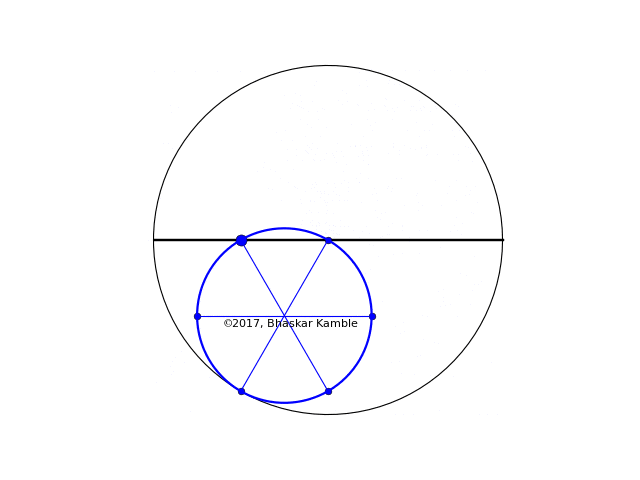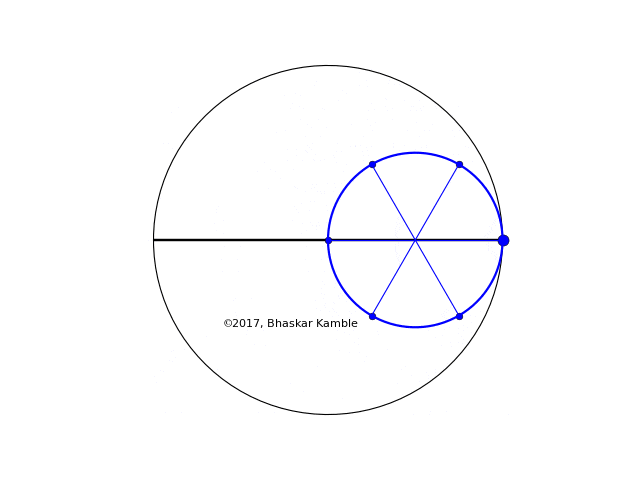
Fig. 10 with $r=R/2$
Epicycloids¶
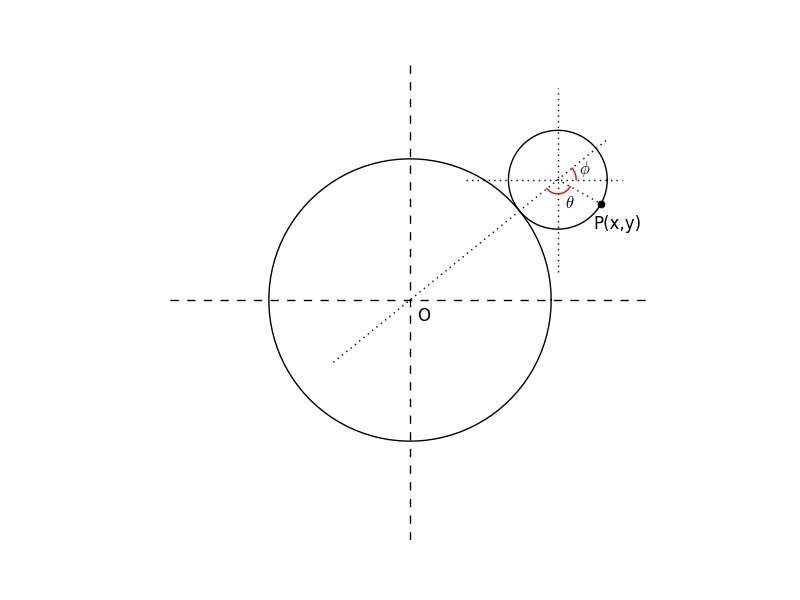
Fig. 11
In this case also w ehave a circle rolling along another circle, with the difference that the rolling circle rolls on the exterior of the fixed circle. The parametric equation is:
\begin{eqnarray} x &=& (R+r)\cos\phi - r\cos\left[ \left( \frac{R}{r} + 1\right)\phi\right] \nonumber \\ y &=& (R+r)\sin\phi - r\sin\left[ \left( \frac{R}{r} + 1\right)\phi\right] \end{eqnarray}
which is simply obtained by replacing $r$ with -$r$ in the hypocycloid equations.
The following shows the special case of a cardioid, which is obtained when both the fixed and moving circles have the same radius.
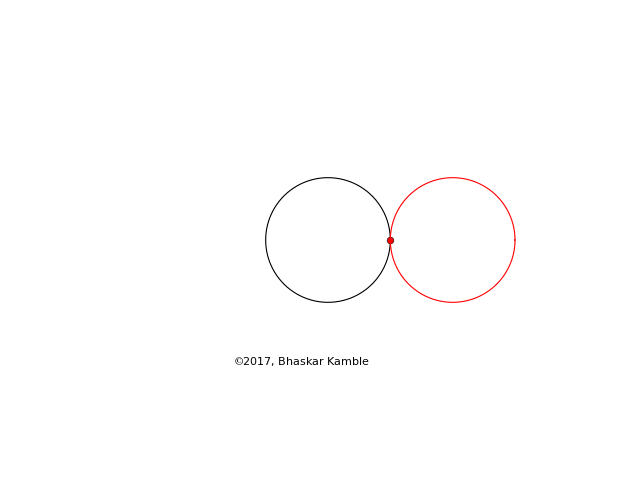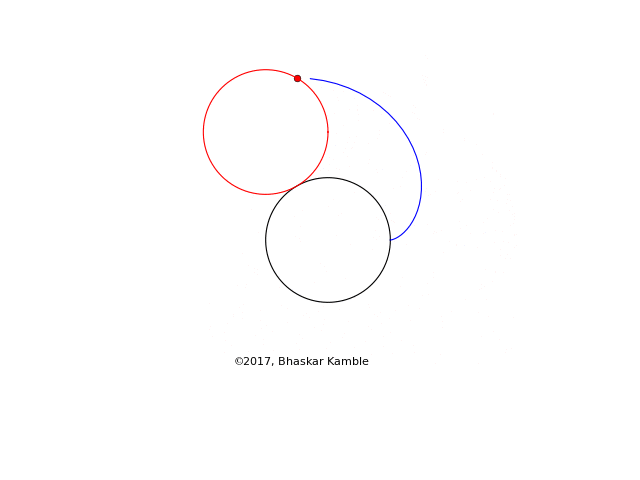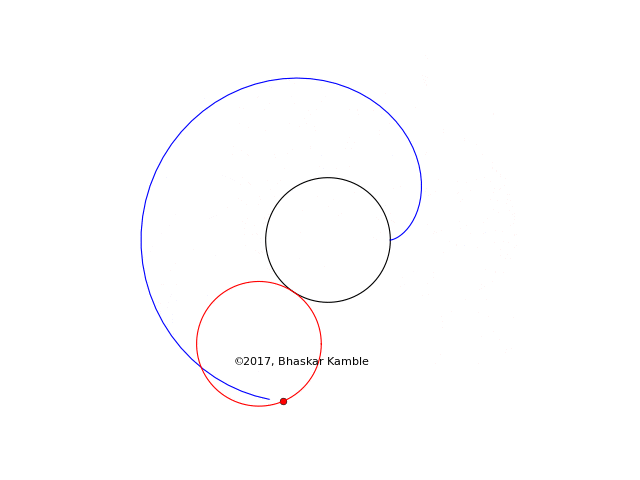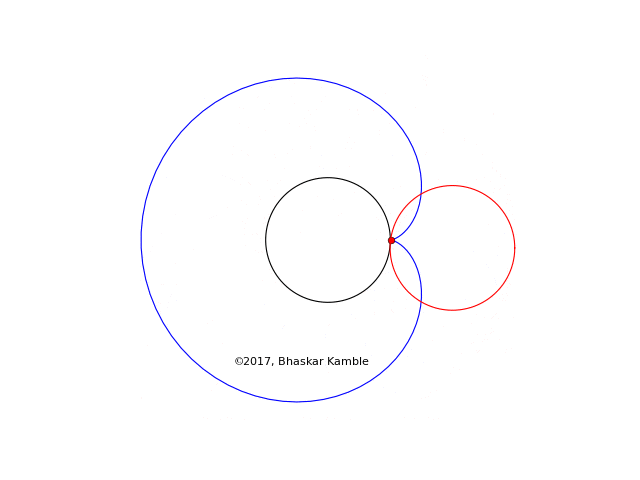
Fig. 12
In spite of its rather boring shape, the cardioid has several very interesting properties which are very nicely described on the wikipedia page.
Since we’ve already seen many animations in the hypocycloid section, maybe just a few in this epicycloid section will suffice. I have animated the cases r = R/5, 2R/5, 3R/5 and 4R/5. The case of r = 5R/5 = R will of course give the cardioid, so I’m not showing it here. It is immediately apparent from the animation that we get four unique curves from the four values of r, as opposed to the hypocycloid case where we obtained only two unique curves from the four values of r (for the hypocycloid r = R/5 and 4R/5 give one of the two unique curves, while r = 2R/5 and 3R/5 give the other curve).
Fig. 13 Top left: $r=R/5$, Top right: $r=2R/5$, Bottom left: $r=3R/5$, Bottom right: $r=4R/5$
Further animations¶
We have already seen that the epicycloid equation is obtained from the hypocycloid equation just by changing the sign of $r$ in the former equation. But what happens when the moving circle in the hypocycloid is bigger than the fixed circle? The moving circle will obviously not be inside the fixed circle in this case, and the curve will be traced outside the fixed circle. Actually, the resulting hypocycloid turns out to be equivalent to an epicycloid! The radius of the circle generating this epicycloid must be equal to the difference of the radius of the large moving circle and the radius of the fixed circle.
The following animation demonstrates this for the specific case of $r_{hypo}=8R/5$, i.e. it shows the hypocycloid which a circle with this radius (the red circle) will produce and the epicycloid which a circle with radius $8R/5-R=3R/5$ (the blue circle) will produce. Following is with hypo_epi_simult_3_spokes.py:
Fig. 14
In Fig. 14, the points fixed to the rims of the two circles always coincide, so one cannot tell them apart. Hence I decided to show the above case again, but this time with sense of rotation of the two circles being opposite. Following is with hypo_epi_simult_3_spokes.py:
Fig. 15
And since they are so pretty, I decided to include one more animation:
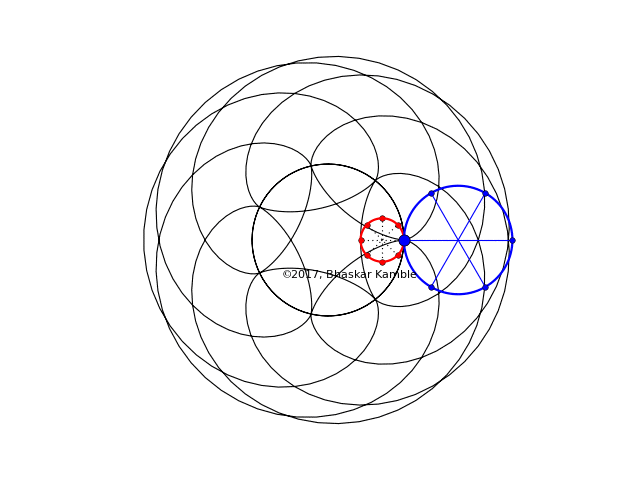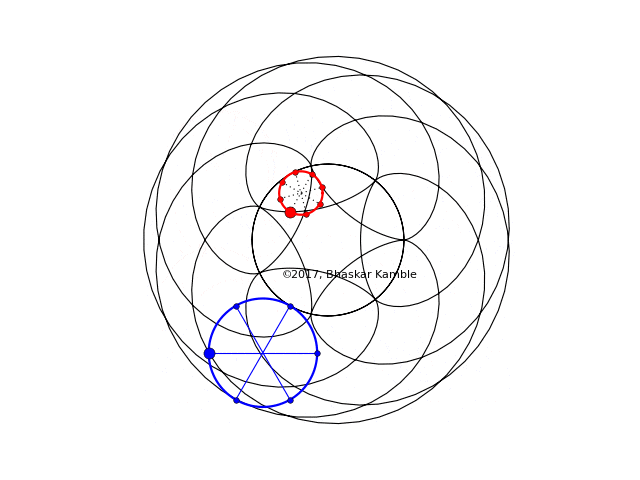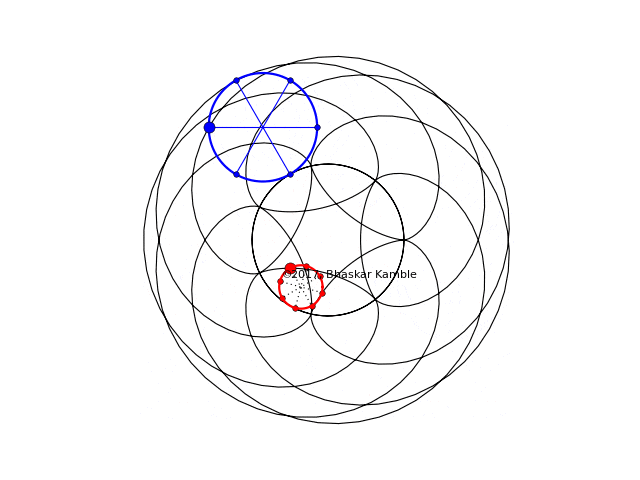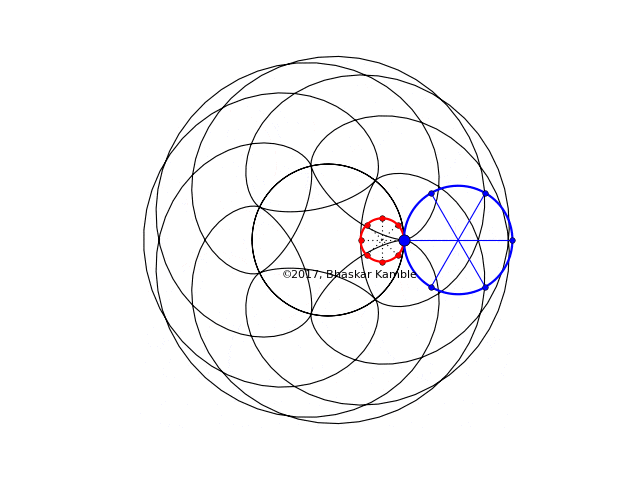
Fig. 16
Further references and links:¶
- https://en.wikipedia.org/wiki/Cardioid (for interesting properties of the cardioid)
- https://de.wikipedia.org/wiki/Epizykloide (this is the german wikipedia site for epicycloids. I include it here because it shows that the evolute of an epicycloid is also an epicycloid.)
- http://demonstrations.wolfram.com/SphereWithTunnelBrachistochrone/ (this is fascinating because it mentions (without proof) that a hypocycloid going through the earth is the shortest time path between two points on the surface of the earth compared to all other underground paths. In a uniform gravitational field the shortest time is the cycloid.)
- https://sourceforge.net/p/geofun/wiki/Home/ (some nice artwork based on these and related curves)
- http://www.v-jaekel.de/animate-trochoid-en.html (an interactive website for generating such curves.)
- http://blogs.ams.org/visualinsight/2013/12/01/deltoid-rolling-inside-astroid/
- https://johncarlosbaez.wordpress.com/2013/12/03/rolling-hypocycloids/ (this and the previous link show some rather amazing properties of hypocycloids based on group theory.)