1. Abstract¶
This article introduces the idea of Fourier series from the approach of linear algebra. Starting with a system of coupled oscillators and introducing the idea of normal modes, the article shows how the wave equation and the Fourier series solution for different boundary conditions are natural consequences of the aforementioned system in the continuum limit. This approach to waves and Fourier series from a purely linear algebra perspective is usually not emphasized and can be an interesting way to revisit the topic.
2. Introduction¶
The subject of the normal modes of a discrete system of coupled oscillators and the Fourier series solution for the wave equation in a continuous medium play a central role in several branches of physics and engineering, and are also important from a pedagogic point of view. A number of articles have been published on the topic of normal modes of discrete systems, which have mainly dealt with the experimental observation of normal modes [1,2] and theoretical analyses of normal modes of finite one-dimensional lattices [3-10]. Interesting extensions to the quantum regime were carried out [11], and systems such as a spring with a finite mass [12,13], the Wilberforce pendulum [14] were also considered. Results of matrix algebra were applied to investigate normal mode analyses in linear spring-mass lattices where the end springs have arbitrary constants [8], as well as for triatomic chains [9] and defect lattices [10].
Likewise, there have been several publications dealing with the oscillations of continuous systems and the Fourier spectrum analyses for these systems. These include experimental set-ups for demonstrating normal modes in strings and air-columns [15-17], illustrating the harmonic content of plucked strings through the Fast Fourier Transform (FFT) and high-speed photography [18-19], theoretical analyses of decay in plucked strings [20], and the modes of a compound string [21]. Fourier series expansion and an expansion in terms of Chebyshev polynomials were used to study inhomogeneous strings [22] as well, and uncertainty relations for Fourier transforms and Fourier series were obtained [23] paralleling the famous uncertainty relations of quantum mechanics.
While the above publications are fascinating and interesting, what has been lacking is the connection between normal modes of a discrete system and the Fourier series solution for waves in a continuous medium. This is surprising considering that while the transition from Fourier series to the Fourier transform is generally well known, the topic of waves and the subsequent Fourier series solution for different boundary conditions is introduced directly starting with the continuum case without emphasizing its connection with the normal modes of a discrete system. However, a discrete system is intuitively simpler to understand, and it therefore appears natural to approach the topic of waves and Fourier series as an extension of this system. Armed with just the basic knowledge of the simple harmonic oscillator and some linear algebra, it is possible to show this connection, and that is precisely the aim of this article.
The outline of this article is as follows: in Section I we recall the general properties of normal modes of a coupled oscillator system. In Section II we state the normal modes for a spring-mass for different boundary conditions. In Section III we recall the wave equation and the Fourier series solution for different boundary conditions. In Section IV we see how the discrete case transforms to the continuum case for the different boundary conditions, and we end with a summary in Section VI.
3. General features of coupled oscillators¶
Suppose a system of $N$ coupled masses constrained to move along the ${\bf {\hat x}}$ direction, with $u_n(t){\bf {\hat x}}$ being the displacement of the $n$th mass from equilibrium, has for the equation of motion \begin{eqnarray} \ddot{u}_n(t) = \sum_{m=1}^N A_{nm}u_m(t), {\hspace 5cm} (1) \label{eom} \end{eqnarray} where ${\bf A}$ is a Hermitian matrix and ${\bf u}$ is an $N$-dimensional column vector of the displacements $u_n(t)$. Then the unitary transformation \begin{equation} \alpha_m(t) = \sum_{n=1}^N S_{mn}u_n(t), {\hspace 5cm} (2) \label{normal_modes} \end{equation} where the columns of ${\bf S^\dagger}$ are the eigenvectors of ${\bf A}$ and ${\bm \alpha}$ is the $N$-dimensional column vector consisting of the normal modes has a solution which can be written in the following two equivalent ways \begin{eqnarray} \alpha_m (t) &=& A_m \cos \omega_mt + B_m \sin \omega_mt, \nonumber \\ \alpha_m (t) &=& A_m \exp (i\omega_m t), {\hspace 5cm} (3) \label{solutions} \end{eqnarray} where $\omega_m= \sqrt{-\lambda_m}$. In the first of the above equations, $A_m$ and $B_m$ are real, while $A_m$ in the second equation is complex. Here we assume that $\lambda_m$, the $m$th eigenvalue of ${\bf A}$, is negative.
Using the unitarity of ${\bf S}$, Eq. (2) can be inverted to give \begin{equation} u_n(t) = \sum_{m=1}^N S_{mn}^* \alpha_m(t). {\hspace 5cm} (4) \label{normal_modes_inverted} \end{equation}
If only one normal mode is present, i.e., if $A_m=\delta_{mm'}A_m$ in the complex form of Eq. (3), then from Eq. (4),
\begin{equation} u_n(t)=A_{m'}S^* _{m'n}\exp(i\omega_{m'}t). {\hspace 4cm} (5) \label{single_mode} \end{equation} Hence, in a normal mode, all the masses oscillate with the same frequency of the normal mode, and the amplitudes and phase differences are given by the eigenvector of the normal mode.
4. Normal modes for different boundary conditions¶
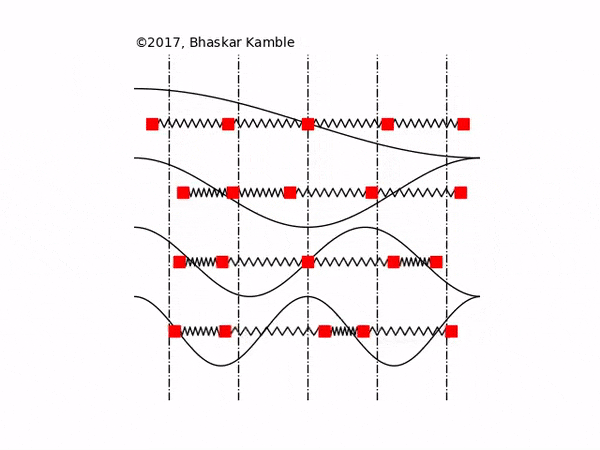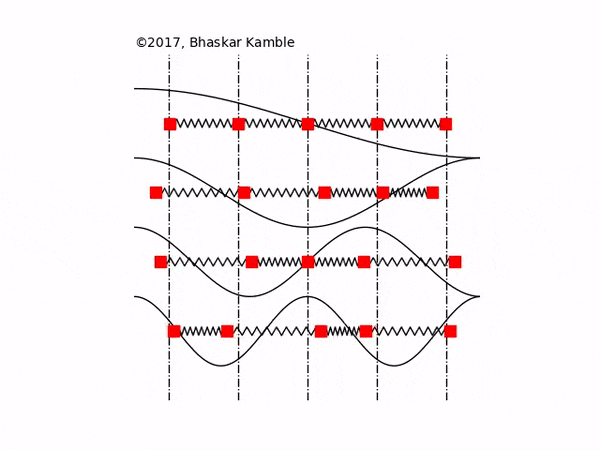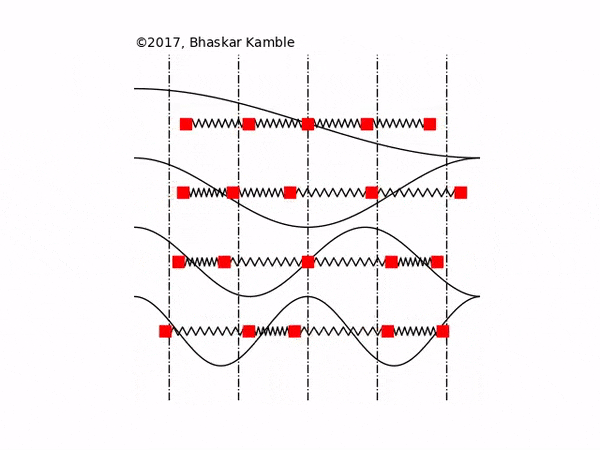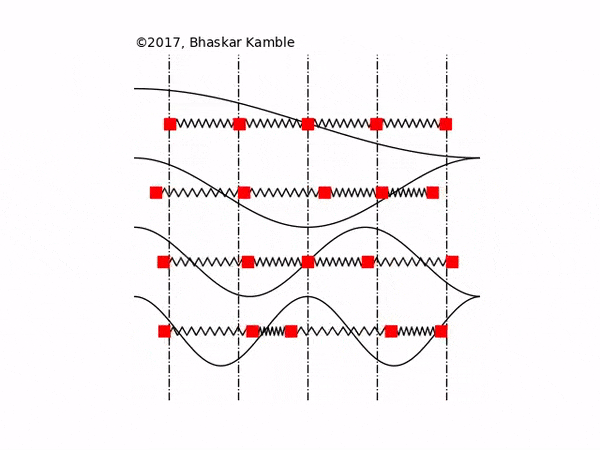
In this section the normal modes of a chain of $N$ identical masses, each of mass $M$ and inter-mass separation $a$, coupled to one another with identical springs with spring constant $K$, are presented for fixed, open and periodic boundary conditions. Fig. \ref{figuremodes} these boundary conditions for $N=4$ masses. Although some of these results have been discussed earlier, we present them here for the sake of clarity and maintaining continuity with the sections that follow.
4.1 Fixed boundary conditions¶
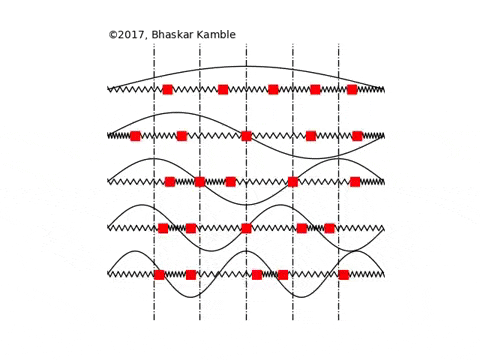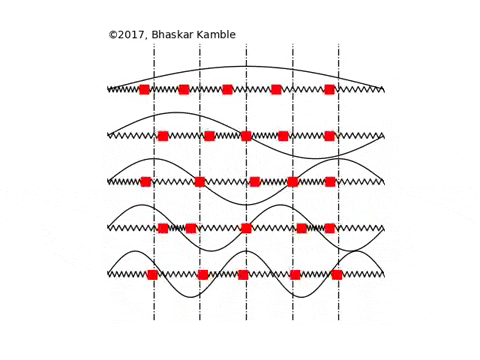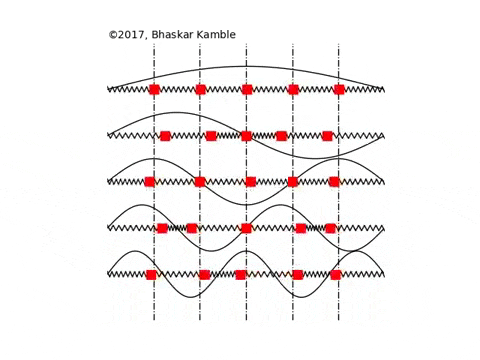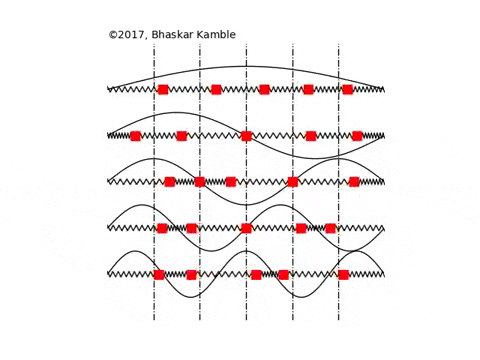
For these boundary conditions, the masses at the end points are attached to rigid walls with the identical springs, as shown in the above animation for $N=5$ masses.
In this case, the matrix ${\bf A}$ in Eq. (1) is \begin{eqnarray} {\bf A} = -\frac{K}{M} \left( \begin{array}{rrrrr} 2 & -1 & 0 & \cdots & 0 \\ -1 & 2 & -1 & \cdots & 0 \\ 0 & -1 & 2 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & -1 \\ 0 & 0 & 0 & -1 & 2 \end{array} \right), \label{matrix_fixed} {\hspace 3cm} (6) \end{eqnarray}
which is proportional to a tridiagonal matrix with $2$ on the diagonals and $-1$ on the upper and lower diagonals. The normal modes are given by Eq. (2), where the column vectors of ${\bf S}^\dagger$ are the eigenvectors of ${\bf A}$. It can be verified that if we choose
\begin{equation} S^\dagger_{nm} = S_{mn}^* = \sqrt{\frac{2}{N}} \sin \frac{mn\pi}{N+1}, {\hspace 4cm} (7) \label{amn_fixed} \end{equation}
then the $m$th column vector of ${\bf S}^\dagger$ is an orthonormal eigenvector of ${\bf A}$ with the eigenvalue $\lambda_m=-\omega_m^2$, where
\begin{equation} \omega_m = \sqrt{\frac{2K}{M} \left( 1-\cos \frac{m\pi}{N+1} \right)}=\sqrt{\frac{4K}{M}}\left| \sin\frac{m\pi}{2(N+1)}\right| {\hspace 2cm} (8) \label{freq_fixed} \end{equation} is the frequency of the mode $m$.
The form for $S_{mn}^*$ in Eq. (7) has been discussed, for example, in the book by Pain [27].
For {\it any} integer $m$, the above system has exactly $N$ non-trivial modes, which follows from the observation that the modes $m$ and $2(N+1)-m$ are identical. Since the eigenvectors are purely real, it follows from Eq. (5) that the normal modes are standing waves with no phase difference between the masses. Physically, Eq. (7) means that the amplitudes of the masses in the $m$th normal mode are modulated with a wavelength $2(N+1)a/m$, as shown in Fig. \ref{figuremodes}(a).
{\bf Historical note.} In the $m$th normal mode, the motion of the $n$th mass is $u_{mn}(t)=S_{mn}^*\exp(i\omega_mt)$, so that for $n\neq 1,N$, $S_{mn}^*$ satisfies the recursion relation \begin{equation} S_{m,n-1}^*+S_{m,n+1}^*+\left( \omega_m^2 \frac{M}{K}-2 \right)S_{mn}^*=0. {\hspace 2cm} (9) \end{equation} $S_{mn}^*$ given by Eq. (7) is one choice which satisfies the above equation and is a special case of the trigonometric relation $\sin(\theta+2\alpha)=2\cos\alpha\sin(\theta+\alpha)-\sin\theta$. Hence if $\cos\alpha$, $\sin\theta$, and $\sin(\theta+\alpha)$ are known, this relation can be used to recursively find $\sin(\theta+2\alpha)$, $\sin(\theta+3\alpha)$, etc. This property was used extensively in ancient India to create sine and cosine tables [25].
4. 2 Open boundary conditions¶
For these boundary conditions, the masses at the end points are free and interact only with their neighbors in the interior, as shown in Fig. \ref{figuremodes}(b) for $N=4$ masses.
In this case, the matrix ${\bf A}$ in Eq. (1) is given by \begin{eqnarray} {\bf A} = -\frac{K}{M} \left( \begin{array}{rrrrr} 1 & -1 & 0 & \cdots & 0 \\ -1 & 2 & -1 & \cdots & 0 \\ 0 & -1 & 2 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & -1 \\ 0 & 0 & 0 & -1 & 1 \end{array} \right). \label{matrix_open} {\hspace 3cm} (10) \end{eqnarray} This is similar to the tridiagonal matrix for fixed boundary conditions, except that the first and last diagonal elements are different. The system now is an isolated system with zero external force, and hence with zero acceleration of the center of mass. This results in one more equation, and hence the degrees of freedom, and therefore the number of nontrivial normal modes are reduced to $N-1$.
To find the normal modes, it can be verified that if we choose
\begin{equation} S_{mn}^* = \sqrt{\frac{2}{N}} \cos \left[ \frac{m\pi}{N} \left( n-\frac{1}{2} \right) \right], \label{amn_open} {\hspace 4cm} (11) \end{equation}
then the $m$th column of ${\bf S}^\dagger$ will be an orthonormal eigenvector of ${\bf A}$ with the eigenvalue $\lambda_m=-\omega_m^2$, where
\begin{equation} \omega_m = \sqrt{\frac{2K}{M} \left( 1-\cos \frac{m\pi}{N} \right)}=\sqrt{\frac{4K}{M}}\left|\sin \frac{m\pi}{2N} \right| \label{freq_open} {\hspace 3cm} (12) \end{equation} is the frequency of the mode $m$.
The form for $S_{mn}^*$ in Eq. (11) has been discussed earlier in the context of finite one dimensional diatomic lattices [4], lattices with periodic impurities [5], and lattices with single mass defects [6].
For {\it any} integer $m$, the mode $m+N$ is identical to the mode $N-m$, resulting in only $N$ unique modes. Of these, one is the trivial mode described by either $m=0$ or $N$, and the rest are the $N-1$ non-trivial modes. From Eq. (5), it follows that the normal modes are standing waves with no phase difference between the masses. Physically, Eq. (11) means that the amplitudes of the masses in the $m$th normal mode are modulated with a wavelength $2Na/m$, as shown in Fig. \ref{figuremodes}(b).
One can also have additionally, "mixed" boundary conditions, where one of the ends is attached to a wall with a spring and the other end is free. In this case, the amplitude of the $n$th mass in the $N$th normal mode is given by $\sin [(n\pi (2m-1))/(2N+1)]$, which can also be guessed from Figs. \ref{figuremodes}(a) and (b). This boundary condition has been discussed in the context of a spring of finite mass with a mass at one of its end points and the other one fixed. [13]
4.3 Periodic boundary conditions¶
In this case we assume that the $N$th mass is coupled back to the first mass with a spring. This is equivalent to the case of an infinite number of masses where the motion of the $n$th mass is identical to that of the $n+N$th mass [26]. Fig. \ref{figuremodes} (c) illustrates this boundary condition for $N=4$ masses.
For these boundary conditions, \begin{eqnarray} {\bf A} = -\frac{K}{M} \left( \begin{array}{rrrrr} 2 & -1 & 0 & \cdots & -1 \\ -1 & 2 & -1 & \cdots & 0 \\ 0 & -1 & 2 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & -1 \\ -1 & 0 & 0 & -1 & 2 \end{array} \right). \label{matrix_periodic} {\hspace 3cm} (13) \end{eqnarray}
This looks similar to the matrix for fixed boundary conditions, but now because of the $-1$ in the top right and bottom left positions, it is no longer tridiagonal. In this case, it can be verified by direct substitution that if $x^N=1$, then the column vector $(1/\sqrt{N})(1,x,x^2,\cdots,x^{N-1})^T$ is an eigenvector with the eigenvalue $2-x-x^{N-1}$. Since $x$ is one of the $N$th roots of unity, we have $x= \exp(2\pi im/N)$ for $m=0,1,2,\cdots N-1$. Hence if we choose
\begin{equation} S_{mn}^* = \frac{1}{\sqrt{N}} \exp \left( \frac{2\pi im(n-1)}{N} \right), \label{amn_periodic} {\hspace 4cm} (14) \end{equation}
the $m$th column of ${\bf S}^\dagger$ is an orthonormal eigenvector of ${\bf A}$ with the eigenvalue $\lambda_m=- \omega_m^2$, where
\begin{equation} \omega_m = \sqrt{\frac{2K}{M}\left( 1-\cos \frac{2\pi m}{N} \right)} = \sqrt{\frac{4K}{M}}\left| \sin\frac{m\pi}{N} \right| \label{freq_periodic} {\hspace 2cm} (15) \end{equation}
is the frequency of the mode $m$. The form for $S_{mn}^*$ in Eq. (14) has been discussed earlier\cite{vonkarman}.
For {\it any} integer $m$, the mode $m$ is identical to the $m+N$ mode. Hence it follows that there are only $N$ modes, of which one is the trivial mode with zero frequency. Since each term in a given eigenvector has the same magnitude, it follows from Eq. (\ref{single_mode}) that each mass in a normal mode has the same amplitude but a different phase, so that the normal modes are traveling waves. Physically, Eq. (14) means that the phases of the masses in the $m$th normal mode modulate with a wavelength $Na/m$, as shown in Fig. \ref{figuremodes}(c).
5. The wave equation in one dimension¶
The wave equation in one dimension reads \begin{equation} \frac{\partial^2 u}{\partial x^2} = \frac{1}{c^2} \frac{\partial^2 u}{\partial t^2}. \label{wave_eqn} {\hspace 4cm} (16) \end{equation}
The general solution for fixed boundary conditions, $u(0,t)=u(L,t)=0$, is
\begin{equation} u(x,t) = \sum_{m=1}^\infty \sin k_m x (A_m \cos \omega_m t + B_m \sin \omega_m t) \label{fourier_series_fixedBC} {\hspace 2cm} (17) \end{equation} with \begin{eqnarray} k_m&=&m;\pi/L \nonumber \\ \omega_m&=&ck;_m, \label{k_and_w} {\hspace 4cm} (18) \end{eqnarray}
where the Fourier coefficients are given by
\begin{eqnarray} A_m &=& \frac{2}{L} \int_0^L \sin (k_mx) u(x,0) dx \nonumber \\ B_m &=& \frac{2}{L\omega_m} \int_0^L \sin (k_mx) \frac{\partial}{\partial t}u(x,0) dx. \label{fourier_coefficients_fixed} {\hspace 2cm} (19) \end{eqnarray}
For open boundary conditions ($\partial u(x,t) / \partial t = 0$ at $x=0,L$) the solution is
\begin{equation} u(x,t) = \sum_{m=1}^\infty \cos k_m x (A_m \cos \omega_m t + B_m \sin \omega_m t) \label{fourier_series_openBC} {\hspace 1cm} (20) \end{equation}
with the Fourier coefficients given by
\begin{eqnarray} A_m &=& \frac{2}{L} \int_0^L \cos (k_mx) u(x,0) dx \nonumber \\ B_m &=& \frac{2}{L\omega_m} \int_0^L \cos (k_mx) \frac{\partial}{\partial t}u(x,0) dx \label{fourier_coefficients_open} {\hspace 2cm} (21) \end{eqnarray}
and $k_m$ and $\omega_m$ given by Eq. (18). For periodic boundary conditions ($u(x,t)=u(x+L,t)$), the solution is
\begin{eqnarray} u(x,t) &=& \sum_{m=1}^{\infty} [\cos k_mx(A_m^{(c)}\cos\omega_mt+B_m^{(c)}\sin\omega_mt) \nonumber \\ &+& \sin k_mx (A_m^{(s)}\cos\omega_mt+B_m^{(s)}\sin\omega_mt)] \label{fourier_series_periodic} {\hspace 4cm} (22) \end{eqnarray} with \begin{eqnarray} k_m&=&2m\pi/L \nonumber \\ \omega_m&=&ck;_m, \label{k_and_w_periodic} {\hspace 4cm} (23) \end{eqnarray} where the Fourier coefficients are given by \begin{eqnarray} A_m^{(c)} &=& \frac{2}{L} \int_0^L \cos (k_mx) u(x,0) dx \nonumber \\ B_m^{(c)} &=& \frac{2}{L\omega_m} \int_0^L \cos (k_mx) \frac{\partial}{\partial t}u(x,0) dx \nonumber \\ A_m^{(s)} &=& \frac{2}{L} \int_0^L \sin (k_mx) u(x,0) dx \nonumber \\ B_m^{(s)} &=& \frac{2}{L\omega_m} \int_0^L \sin (k_mx) \frac{\partial}{\partial t}u(x,0) dx. {\hspace 4cm} (24) \nonumber \\ \label{fourier_coefficients_periodic} \end{eqnarray}
In the following section we will see how the above results are obtained as the limiting case of the spring-mass system considered earlier.
6. The continuum limit of the discrete case¶
It follows from Eq. (1), (6), (10), and (13) that, regardless of the boundary conditions, the equation of motion of a mass not at the end points (i.e. $n\neq 0,N$) can be rewritten as \begin{equation} {\ddot u}_{n} = \frac{Ka^2}{M} \left [\frac{\left( \frac{u_{n+1}-u_n}{a} \right) - \left( \frac{u_n-u_{n-1}}{a} \right)} {a} \right], {\hspace 4cm} (25) \end{equation} where $a$ is the inter-mass separation. In the continuum limit, we keep the distance $L$ fixed but let $N\rightarrow\infty$. Then the above approaches the wave equation Eq. (16), with \begin{equation} c = a\sqrt{\frac{K}{M}}. {\hspace 4cm} (26) \label{speed_sound} \end{equation}
Elementary derivations of the speed of waves in solids, fluids, and a string were published in an early paper which used the conventional approach of starting straightaway from the continuum case [24]. Alternatively, one can start from the discrete spring-mass system used in this article to arrive at the same results. For example, the longitudinal waves of an air-column can be modeled by considering a number of such identical, independent
systems arranged parallelly in a cylinder of length $L$, such that all the masses at a particular cross-section move exactly in phase. Then the bulk modulus $B$ (which equals $-VdP/dV$, with $P$ and $V$ being the pressure and volume, respectively) can be shown to be $N_SKa/S$, where $S$ is the area of cross-section, and $N_S$ is the number of masses in the cross-section.
This can be seen as follows. Suppose that the springs on the left of a particular cross section of masses have a length $l$ at some time $t$. Then the force due to {\it these} springs on the masses is $N_SK(a_0-x)$, where $a_0$ is the unstretched length of a spring, so that the pressure on the left is $P=N_SK(a_0-l)/S$. The volume enclosed between this cross section, the cross section adjacent to it on the left, and the cylinder is $V=lS$. Then the incremental changes in the pressure and volume due to an incremental change in $l$ are, respectively, $dP=-(N_SK/S)dl$ and $dV=Sdl$. Hence the bulk modulus, $-VdP/dV$, equals $N_SKa/S$, where we have taken for $V$ its equilibrium value, $Sa$.
Similarly, the density $\rho$ is $N_SM/Sa$, so that in the continuum limit, Eq. (26) turns to be $\sqrt{B/\rho}$, which is the well known formula for the speed of sound in air.
In this article we will stick to the spring-mass system where the masses move longitudinally. However, the analysis remains the same for transverse oscillations, where the spring-mass system now approaches a string in the continuum limit. The only thing which changes is the constant $-K/M$ in front of the matrices of Eq. (6), (10), and (13), which is now replaced by $-Kd/Ma$, where $d$ is the change in length of a {\it single} spring compared to its equilibrium length. For this case, $c$ in Eq. (26) is replaced by $\sqrt{Kda/M}$, which in the continuum limit is easily seen to be $\sqrt{T/\lambda}$, with $T$ and $\lambda$ being the tension and linear mass density of the string, respectively.
Recent experiments have been devised to illustrate the harmonic content of plucked guitar strings [18] and to see the vibrational pattern of a string using high-speed photography [19]. In passing we also mention that while strings are generally used to illustrate normal modes with fixed boundary conditions, an interesting experiment was devised to observe normal modes in strings with open boundary conditions [15].
6.1 Fixed boundary conditions¶
Using Eq.(4), which gives the motion in terms of the normal modes, and real version of the normal mode solutions, Eq. (3), and Eq. (7), which gives the amplitudes of the masses in a normal mode, gives \begin{equation} u_n(t) = \sum_{m=1}^N \sin \frac{nm\pi}{N+1} ({\tilde A}_m\cos \omega_mt + {\tilde B}_m \sin \omega_mt), {\hspace 4cm} (27) \label{fixed_expansion} \end{equation} where ${\tilde A}_m=\sqrt{\frac{2}{N}}A_m$ and ${\tilde B}_m=\sqrt{\frac{2}{N}}B_m$, and where $\omega_m$ is given by Eq. (8).
Now we take the $N\rightarrow \infty$ limit for a fixed, finite $L$. In this limit, using $\sin x \approx x$ for small $x$ in Eq. (8), gives for the frequency $\omega_m=ck_m$, with $c$ given by the limiting value of Eq. (26). Next, using $(N+1)a=L$, and defining $k_m=m\pi/La$, and associating the point $na$ with space point $x$, Eq. (27) becomes, in the continuum limit, \begin{equation} u(x,t) = \sum_{m=1}^\infty \sin k_mx \left( {\tilde A}_m\cos \omega_mt + {\tilde B}_m\sin \omega_mt \right), {\hspace 4cm} (28) \end{equation} which is exactly the Fourier series expansion for $u(x,t)$ for fixed boundary conditions (Eq. (17-18)).
Now we find the Fourier coefficients ${\tilde A}_m$ and ${\tilde B}_m$. Using the real form of Eq. (3), which gives the general solution of the normal modes, in Eq. (2), which gives the normal modes in terms of the motion of the masses, and with Eq. (7), which gives the amplitudes of the masses in a normal mode, we have \begin{equation} A_m \cos \omega_m t + B_m \sin \omega_m t = \sqrt{\frac{2}{N}} \sum_{n=1}^N \sin \left( \frac{mn\pi}{N+1} \right)u_n(t). {\hspace 4cm} (29) \label{thirtyfive} \end{equation} Putting $t=0$, and noting that for large $N$, $Na \approx (N+1)a=L$, we get \begin{equation} {\tilde A}_m=A_m \sqrt{\frac{2}{N}} = \frac{2}{L} \sum_{n=1}^N \sin \left( \frac{m(na)\pi}{L} \right)u_n(0) a. {\hspace 4cm} (30) \end{equation} Now taking the $N\rightarrow \infty$ limit, and associating $na$ with $x$, the above becomes \begin{equation} {\tilde A}_m = \frac{2}{L} \int_0^L \sin \left( \frac{mx\pi}{L} \right)u(x,0)dx. {\hspace 4cm} (31) \end{equation} Similarly, ${\tilde B}_m$ is found by differentiating Eq. (29) with time and putting $t=0$. This gives \begin{equation} {\tilde B}_m = \frac{2}{L\omega_m} \int_0^L \sin \left( \frac{mx\pi}{L} \right) \left. \frac{\partial u(x,t)}{\partial t} \right|_{t=0} dx. {\hspace 4cm} (32) \end{equation} The above coefficients are exactly as those given by Eq. (19).
6.2 Open boundary conditions¶
For open boundary conditions, an analysis, exactly similar to the case of fixed boundary conditions, leads, in the continuum limit, to the following Fourier series for $u(x,t)$: \begin{equation} u(x,t) = \sum_{m=1}^\infty \cos k_m x \left({\tilde A}_m\cos \omega_mt + {\tilde B}_m \sin \omega_mt \right) {\hspace 4cm} (33) \end{equation} with $k_m$ and $\omega_m$, as in the case of fixed boundary conditions, given by $k_m=m\pi/L$ and $\omega_m=ck_m$, and $c$ given by the limiting value of Eq. (26). In this case, space point $x$ must be associated with $(n-1/2)a$. The Fourier coefficients are also found exactly in the same manner as that used in the case of fixed boundary conditions, and turn out to be \begin{eqnarray} {\tilde A}_m &=& \frac{2}{L} \int_0^L \cos \left( \frac{mx\pi}{L} \right)u(x,0)dx \nonumber \\ {\tilde B}_m &=& \frac{2}{L\omega_m} \int_0^L \cos \left( \frac{mx\pi}{L} \right) \left. \frac{\partial u(x,t)}{\partial t} \right|_{t=0} dx. {\hspace 4cm} (34) \end{eqnarray} The above is identical to the Fourier series for open boundary conditions given by Eqs. (20-21).
6.3 Periodic boundary conditions¶
In this case the wave number and frequency are given by Eq. (23). The complex nature of the eigenvectors (Eq. (14)) in this case suggests that we should use the complex version of Eq. (3). Assuming only mode $m$ is present, we have $u_n(t)\sim \exp[i(2\pi mx_n/Na + \omega_mt)]$, where $x_n=(n-1)a$ is the position of the $n$th mass. This is a wave traveling in the $-x$ direction with $\omega_m$ given by Eq. (15) and wave number $2\pi m/Na$. Similarly, it can be verified that the mode $N-m$ is also a wave with the same frequency and wave number but traveling in the $+x$ direction. Since one of the modes is a trivial mode, it follows that if $N-1$ is even, then for each non-trivial mode of a given frequency, there is another mode of the same frequency but representing a wave traveling in the opposite direction, resulting in $(N-1)/2$ unique frequencies, apart from the frequency of the trivial mode. On the other hand, if $N-1$ is odd, then the mode $m=N/2$ is such that any two adjacent masses oscillate exactly out of phase, and hence the wave motion cannot be assigned a specific direction. Leaving this mode and the trivial mode aside, the rest of the $N-2$ modes can be divided into two groups: one consisting of waves traveling in the positive direction and the other in the negative direction.
For simplicity consider the case where $N-1$ is even. Since the mode $m$ is equivalent to the $m-N$ mode, we can let $m$ vary from $-(N-1)/2$ to $(N-1)/2$ in Eq. (4) which, using Eq. (14), becomes \begin{equation} u_n(t)= \sum_{m=-(N-1)/2}^{(N-1)/2} {\tilde A}_m \exp \left[i\left(\frac{2\pi m x_n}{Na} + \omega_mt\right)\right], {\hspace 4cm} (35) \label{unt_periodic} \end{equation} where ${\tilde A}_m=\sqrt{\frac{2}{N}}A_m$. (The case of even $N$ can be similarly treated by letting $m$ run from $-N/2$ to $(N/2)-1$.) Using $Na=L$, introducing $k_m=2\pi m/Na$, and associating $x_n$ with $x$, we get in the continuum limit ($N\rightarrow \infty$) \begin{equation} u(x,t)= \sum_{m=-\infty}^\infty {\tilde A}_m \exp \left[i\left(k_m x_n + \omega_mt\right)\right], {\hspace 4cm} (36) \end{equation} where $\omega_m=ck_m$, which follows from Eq. (15) in the continuum limit, with $c$ being given as usual by Eq. (26).
${\tilde A}_m$ can be determined by putting $t=0$ in Eq. (2) and using the complex form of Eq. (3). In the continuum limit this amounts to \begin{equation} {\tilde A}_m=\frac{1}{L}\int_{0}^L e^{-ik_mx}u(x,0)dx. {\hspace 4cm} (37) \label{coefficients_periodic_discrete} \end{equation} To establish the equivalence with Eq. (22-24), Eq. (35) can be expressed purely in terms of the sine and cosine functions: \begin{eqnarray} u_n(t)&=&{\tilde A}0 + \sum{m=1}^{(N-1)/2} \left[ ({\tilde A}m+{\tilde A}{-m})\cos k_mx_n \cos \omega_mt % \right. \nonumber \
+ i({\tilde A}_m+{\tilde A}_{-m}) \cos k_mx_n \sin \omega_mt \right. \nonumber \\
&+& \left. i({\tilde A}_m-{\tilde A}_{-m}) \sin k_mx_n \cos \omega_mt %\nonumber \\
+ (-{\tilde A}_m+{\tilde A}_{-m}) \sin k_mx_n \sin \omega_mt \right].
\label{real_fourier} {\hspace 4cm} (38)
\end{eqnarray} Physically, only $\Re[u_n(t)]$ or $\Re[u(x,t)]$ can be accessed, which means that we need $\Re[{\tilde A}_m+{\tilde A}_{-m}]$, $\Re[i({\tilde A}_m+{\tilde A}_{-m})]$, etc. from the above equation. From Eq. (37) \begin{equation} \Re[{\tilde A}_m+{\tilde A}_{-m}]=\frac{2}{L}\int_0^L \cos (k_mx) \Re [u(x,0)] dx. {\hspace 4cm} (39) \label{real_periodic_1} \end{equation} If we try to use Eq. (37) to find $\Re[i({\tilde A}_m+{\tilde A}_{-m})]$, we will end up requiring the imaginary part of $u(x,0)$. However, the imaginary part of $u(x,t)$ is in general not available. This problem can be solved by taking the time derivative of Eq. (2) and, using Eq. (3) with $t=0$, this yields \begin{equation} i\omega_m {\tilde A}_m = \frac{1}{N}\sum_{n=1}^N e^{-ik_mx_n} \left. \frac{\partial u_n(t)}{\partial t} \right|_{t=0} {\hspace 4cm} (40) \end{equation} where we have also used Eq. (14). Hence in the continuum we get for $\Re[i({\tilde A}_m + {\tilde A}_{-m})]$ \begin{equation} \Re[i({\tilde A}_m+{\tilde A}_{-m})]=\frac{2}{\omega_m L} \int_0^{L} \cos k_mx \times\Re\left[ \left. \frac{\partial u(x,t)}{\partial t} \right|_{t=0} \right]dx. {\hspace 4cm} (41) \label{real_periodic_2} \end{equation} The real part of the other two coefficients in Eq. (38) can be similarly shown to be \begin{equation} \Re[i({\tilde A}_m-{\tilde A}_{-m})] = \frac{2}{L} \int_0^L \sin k_mx \times \Re[u(x,0)] dx {\hspace 4cm} (42) \label{real_periodic_3} \end{equation} \begin{equation} \Re[-{\tilde A}_m+{\tilde A}_{-m}] = \frac{2}{\omega_m L} \int_0^L \sin k_mx \times \Re\left[ \left. \frac{\partial u(x,t)}{\partial t} \right|_{t=0} \right]dx. {\hspace 4cm} (43) \label{real_periodic_4} \end{equation} Eqs. (38,39,41-43) are equivalent to the Fourier series expansion for periodic boundary conditions, given by Eqs. (22-24).
From the above discussion, a basic theorem in digital signal processing, usually known as the Nyquist sampling theorem, becomes clear. The theorem states that if a continuous signal with a finite time period is sampled every $\delta t$ seconds (with $\delta t$ smaller than the time period), then the maximum frequency that will be described by the sampling is $(1/2)\times2\pi/\delta t$. This can be seen as follows. If we associate the equilibrium position of the $n$th mass with the time when the $n$th sample is taken, and the distance $a$ between adjacent masses with the time interval $\delta t$ between two consecutive samples, then $u_n(t)$ at $t=0$ can be compared to the $n$ samples of the signal. Thus, the wave number $k_m=2\pi m/Na$ for the spring mass system is equivalent to the $m$th frequency of the time signal. The maximum value that $k_m$ can take is given by $m=(N-1)/2$ for odd $N$, as seen by Eq. (38), and $N/2$ for even $N$. For the latter case, this equals $\pi/a$, which is half of $2\pi/a$. Comparing to the case of signals using the associations just outlined, this means that the maximum frequency described by the sampling is $\pi/\delta t$, which is half of $2\pi/\delta t$, which is exactly what the theorem says.
{\bf Note added for DFT, 16 October 2016}
Using the same correspondence, further properties of discrete time signals become clear. A real time signal is equivalent to $u_n(0)$ in Eq. (38) with $n$ playing the role of the discrete time index. Further, for $t=0$, only the first and third terms on the right hand side of Eq. (38) survive.
If $u_n(0)$ is real for all $n$, then $A_m+A_{-m}$ and $i(A_m-A_{-m})$, which occur in the first and third terms of Eq. (38), respectively, are real, which implies that $A_{-m}=A_m^*$. In other words $\Re [A_{-m}] = \Re [A_m]$ and $\Im [A_{-m}] = -\Im [A_m]$.
Moreover, if $u_n(0)$ is an even signal, i.e. if $u_{-n}(0)=u_n(0)$, then the third term on the right side of Eq. (38) involving the $\sin k_mx_n$ term vanishes since it is odd in $n$ and only the first term remains. This can happen only if $i(A_m-A_{-m})$ vanishes i.e. if $\Im [A_m]=0$.
Likewise for a signal odd in $n$, the real part of its DFT vanishes ($A_m$ is proportional to DFT).
7. Summary¶
In this article we approached the wave equation and the Fourier series solution for various boundary conditions purely as the limiting case of a system of discrete coupled oscillators. Starting with the discrete system, we obtained the normal modes for three different boundary conditions (fixed, open, and periodic) by diagonalizing the matrix appearing in the respective equation of motion. The amplitudes and phases of the masses in a normal mode are given by the eigenvectors while the frequencies are determined by the eigenvalues. In the continuum limit, the equations of motion approached the wave equation with the speed of the wave given in terms of the limiting values of the system parameters. An arbitrary motion of the masses is a linear combination of the normal modes, with the coefficients determined by the initial conditions. In the continuum limit, this linear combination was shown to be identical to the Fourier series expansion for each of the three boundary conditions separately. The wavenumber and frequency of each Fourier mode were further shown to satisfy the dispersion relation in terms of the speed of the wave, obtained as the limiting value of the system parameters in the continuum limit. Further, it was shown that the coefficients in the normal modes expansion for the discrete system become identical to the Fourier coefficients in the continuum limit for each boundary condition separately.
It is interesting to note that while the exact solutions for the normal modes for the spring-mass system used in this article are well known in the literature for different boundary conditions, the close connection between these normal modes and the Fourier series solution is rarely emphasized. The approach in this article emphasizes this connection in a unified way and can be an interesting way to introduce or to revisit the topic. It can also be used as an initial point to understand other wave phenomena starting from this approach.
Bibliography¶
\begin{thebibliography}{99}
[1] \bibitem{givens} Ryan Givens, O. F. de Alcantara Bonfim and Robert B. Ormond, "Direct observation of normal modes in coupled oscillators", Am. J. Phys. {\bf 71} (1), 87-90 (2003).
[2] \bibitem{kannewurf} C. R. Kannewurf and Harald C. Jensen, "Coupled Oscillations", Am. J. Phys. 25, 442-445 (1957);
[3] \bibitem{band} William Band and A. D. Bhatti, "Energy Propagation in a Finite Lattice", Am. J. Phys. 33, 930-933 (1965).
[4] \bibitem{chaturvedi} D. K. Chaturvedi and J. S. Baijal, "Normal Modes of Oscillation for a Finite One-Dimensional Diatomic Lattice", Am. J. Phys. 42, 482-486 (1974).
[5] \bibitem{lee} S. M. Lee, "Exact Normal-Mode Analysis for a Linear Lattice with “Periodic Impurities", Am. J. Phys. 37, 888-894 (1969).
[6] \bibitem{weinstock} Robert Weinstock, "Normal-Mode Frequencies of Finite One-Dimensional Lattices with Single Mass Defect: Exact Solutions", Am. J. Phys. 39, 484-502 (1971).
[7] \bibitem{weinstock2} Robert Weinstock, "Oscillations of a particle attached to a heavy spring: An application of the Stieltjes integral", Am. J. Phys. 47, 508 (1979)
[8] \bibitem{louck} James D. Louck, "Exact Normal Modes of Oscillation of a Linear Chain of Identical Particles", Am. J. Phys. 30, 585-590 (1962)
[9] \bibitem{kesavasamy1} K. Kesavasamy and N. Krishnamurthy, "Lattice vibrations in a linear triatomic chain", Am. J. Phys. {\bf 46}(8), 815-819 (1978);
[10] \bibitem{kesavasamy2} K. Kesavasamy and N. Krishnamurthy, "Vibrations of a one‐dimensional defect lattice", Am. J. Phys. {\bf 47}(11), 968-973 (1979).
[11] \bibitem{bhattacharya} M. Bhattacharya, H. Shi and S. Preble, "Coupled second-quantized oscillators", Am. J. Phys. {\bf 81}(4), 267-273 (2013)
[12] \bibitem{cushing} James T. Cushing, "The spring‐mass system revisited" Am. J. Phys. {\bf 52}(10), 925-933 (1984); The method of characteristics applied to the massive spring problem, 52, 933 (1984).
[13] \bibitem{bloodmazur} Paul Mazur and Frank A. Blood Jr., "Comparison of Normal Modes of an End-Weighted Discrete and Continuous Linear Chain", Am. J. Phys. 40, 1694-1696 (1972)
[14] \bibitem{berg} Richard E. Berg and Todd S. Marshall "Wilberforce pendulum oscillations and normal modes", Am. J. Phys. {\bf 59}(1), 32-38 (1991).
[15] \bibitem{kashy} E. Kashy, D. A. Johnson, J. McIntyre and S. L. Wolfe, "Transverse standing waves in a string with free ends", Am. J. Phys. {\bf 65}(4), 310-313 (1997).
[16] \bibitem{jihui} D. Jihui and C. T. P. Wang, "Demonstration of longitudinal standing waves in a pipe revisited", Am. J. Phys. 53, 1110 (1985).
[17] \bibitem{ficken} G. Ficken and F. Stephenson, "Comments on the Rubens flame tube", Am. J. Phys. 54, 297 (1986).
[18] \bibitem{perov} Polievkt Perov, Walter Johnson and Nataliia Perova-Mello, "The physics of guitar string vibrations", Am. J. Phys. {\bf 84}(1), 38-43 (2016).
[19] \bibitem{whitfield} Scott B. Whitfield and Kurt B. Flesch, "An experimental analysis of a vibrating guitar string using high-speed photography", Am. J. Phys. {\bf 82}(2), 102-109 (2014).
[20] \bibitem{politzer} David Politzer, "The plucked string: An example of non-normal dynamics", Am. J. Phys. {\bf 83}(5), 395-402 (2015).
[21] \bibitem{rossing} Thomas D. Rossing, "Normal modes of a compound string", Am. J. Phys. {\bf 43}(8), 735-736 (1975).
[22] \bibitem{rawitscher} George Rawitscher and Jakob Liss,"The vibrating inhomogeneous string", Am. J. Phys. {\bf 79}(4), 417-427 (2011).
[23] \bibitem{forbes} G. W. Forbes and M. A. Alonso, "Measures of spread for periodic distributions and the associated uncertainty relations", Am. J. Phys. {\bf 69}(3), 340-347 (2001). ibid., "Consistent analogs of the Fourier uncertainly relation", Am. J. Phys. {\bf 69}(10), 1091-1095 (2001).
[24] \bibitem{oleary} Austin J. O'Leary, "Elementary Derivation of Equations for Wave Speeds", Am. J. Phys. 22, 327-334 (1954).
[25] \bibitem{sineseries} John Playfair, "On the trigonometric tables of the Brahmins", Transactions of the Royal Society of Edinburgh, Vol. IV, 1798.
[26] \bibitem{vonkarman} N. W. Ashcroft and N. D. Mermin, "Solid State Physics", Chapter 22, pp. 430-431, Holt, Rinehart and Winston, New York, 1976.
[27] \bibitem{fixedbc} H. J. Pain, "The Physics of Vibrations and Waves", Chapter 4, pp. 90-95, Sixth Edition, Wiley 2005.
\end{thebibliography}